|
<カオス>
今ここで、ぼくがくしゃみを一つしたとします。
それによって生まれた空気の揺れは、
だんだんと拡散していきますが、
なくなるわけではありません。
ただ限りなく薄く弱くなっていくだけです。
このぼくのくしゃみが、
北京のこの冬の気候になにかしら、
影響をあたえるでしょうか?
答えは、ありうるです。
ぼくがここでくしゃみをがまんしたか、しなかったか、
そんな些細なことが、
遠く離れた場所の未来の天候に影響します。
しかも、どう影響するかは、だ~れにもわからない。
さらに、もし同じ力のくしゃみができたとしたら、
結果(影響)は100%同じになります。
これは、
有名な「バタフライ効果」というものなのですが、
なにも、天候に限らず、そういうイタズラをするのが、
カオスってヤツです。(詳細は、本文を読んで下さい)
※数式多いです。ご注意!
以下、「マッチ箱の脳」の「ニューラルネットワーク」より抜粋
カオス、フラクタル、f分の1ノイズ、ファジー、
ひところこんな言葉がちまたにあふれましたね。
家電製品などの
セールストークに使われていたこともありました。
こうした知名度とはうらはらに、
それらは何であるかについては
あまり知られていないのが現状でしょう。
ま、AIという言葉もそうですが。
そんな中で、特にAIとかかわりが深いカオスについて、
ここでちょっとお話しします。
★カオス登場
さて、カオスです。
カオスという言葉は、
ギリシャ語のkhaosが基になっていますが、
現在では、Chaos(ケイオス:混沌という意味)という
表記が一般的です。
一般的なカオスの定義は次のようになります。
――あるシステムの、
ある時点での状態(=初期値)が決まれば、
その後の状態は原理的にすべて決定される、
という決定論的法則に従っているにもかかわらず、
非常に複雑で不規則かつ不安定な振る舞いをして
遠い将来における状態の予測が不可能な現象がある。
これをカオスであると言う。
……はい、なんだか、
わかったようなわからないような説明ですね。
まさに混沌としています。
はっきりした計算式などで書かれているので、
何が起こるかは厳密に決まっているはずなのに、
その進行の様子が非常に揺らいでいて、
その先どういう値になるのかうまく予想できない現象。
だいたいこういうことなんだと思います。
★カオス的数学の話
我々が学校で習った数式、
例えばy=3(x-2)などは、
xがどんな値になろうが、
yの値は確実に求めることができました。
xが5なら、yは9です。
xが10ならyは24。
xが83759ならyは251271というように、
xがどんな大きな(=未来の)値になろうと
yの値は100%確実にわかります。
我々は、このように数式で書き表せるものは、
必ず未来を(答えを)予測できると思い込んでいます。
例えば、y=3.6x(1-x)なんていう式も、
上の数式と同じように、xがどんな値になろうと、
確実にyの値もわかるだろうと、
数学が苦手な人でも思われることでしょう。
この式は
上に凸な放物線(懐かしい言葉!)を描きますから、
xの値がどんどん大きくなっていくと、
yの値はどんどん小さくなる一方であることも
簡単に予想できます。
そこで、ちょっと目を移して図を見てください。
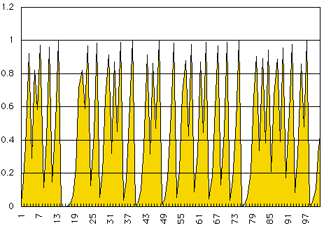
ひどく蛇行したグラフですね。
でたらめな図といっても差し支えないほどです。
実はこのグラフが、
上のy=3.6x(1-x)のグラフだといったら驚きませんか?
詳しい数字は後述しますが、
これは実は、xのところに
その前のyの値を代入するということを
繰り返したときのグラフです。
このグラフを見ると、
ずっと先のyの値はどうなるのか
さっぱりわからないような気がします。
この先、大きな値になっていくのか、
小さな値になっていくのか、
大きくなったり小さくなったりを繰り返すのか、
それすら見当がつきません。
実際に、ずっと先のyの値がどのような値になるかは
全く予測できないのです!
このように、数式としては、はっきりしているのに、
未来の値がどんな値になるのかさっぱりわからない。
逆に言うと、一見、デタラメ(自然?)であるような
振る舞いのように見えながら、
実はきっちりと数式に書き表せる。
そうした現象がカオスということになります。
というと、ただの乱数と同じじゃないかと
思われるかもしれませんが、
乱数が、毎度毎度、
全く違った値になってしまうのに対して、
カオスは、最初の値が同じであれば
100%同じ結論になります。
この点が大きく違います。
★カオスの発見
今後、学校で習う円周率は3.14から3になるそうです。
これは、0.14なんて端数は、
あまり影響がないということなんでしょうね。
生涯を円周率の計算に費やした人には申し訳ないんですが、
確かに、大概の人は、
円周率はだいたい3くらいと知っているだけで
十分という気がします。
1961年、気象学者のローレンツは、
天気予報を正確に予測しようと、
ある方程式を打ち立てて
コンピュータで3回計算したところ、
なんと3回とも全く違う答えが出てきてしまいました。
これはなぜかを調べた結果、
最初の計算は小数点以下を6桁でやっていたのに、
その後の計算(検算)では、
小数点以下を3桁で計算していたことが
原因であるとわかりました。
カオスの存在が知られていなかった当時、
小数点以下が6桁までのデータを、
3桁にしてしまっても、
計算結果には、
あまり影響はないだろうと考えられていました。
そこでローレンツも、
計算を楽にするために
小数点以下を3桁で検算したのでした。
ところがどっこい、
この小数点3桁から6桁までの値の差が、
計算結果にとんでもない
大きな差を生み出してしまったのでした。
皮肉にもこの発見が、気象学における貢献よりも、
ローレンツを有名にしてしまいました。
★カオスの過敏症
例えば、y=4x(1-x)という式を使って調べてみましょう。
このxの、最初の値が0.3だった場合と、
0.3000000001だった場合を考えます。
たった1億分の1しか違わないんですよ!
この2つをそれぞれ計算していったとき、
その後のyの値になんらかの影響を与えると思いますか?
なんと100ステップ後に、yの値は次のようになります。
◆xの最初の値が0.3の場合:0.673899088
◆xの最初の値が0.3000000001の場合:0.076831721
xの最初の値が1億分の1少ないだけなのに、
100ステップ後には9倍弱の値になりました。
一般に、このようなカオス的な振る舞いを起こす数式は、
最初の値のほんのちょっとした違いに非常に敏感です。
こういう症状を「初期値過敏性」と言います。
★バタフライ効果
数式上でどんなことが起ころうと、
我々の日常とは全く関係ないことじゃないと
思われるかもしれませんが、
「バタフライ効果」という、
ちょっと不思議な例え話があります。
――ブラジルで蝶々(バタフライ)が羽ばたくと、
そのときに周りの空気が揺れたり、
あるいは、蝶々が熱を発したりする。
これはとっても微々たる量なんだけれども、
だからといって消えてなくなるモノではなく、
その影響は周りにジワ~~~っと浸透していく。
その影響の連鎖は、やがて気象にも影響を及ぼし、
ついには、数週間後遠く離れた
アメリカのテキサスに竜巻を起こす……
というものです。
ちなみに、原書ではブラジルとテキサスなんですが、
どうしてか、
アマゾンやら北京やらユーヨークやらと
地名が変えられて書かれていることがあります。
たかが蝶々一匹の羽ばたきで、
そんな遠くの天候が変わるなんてと
疑われる方もいるかもしれません。
でも、前述の例のように、
最初の値がたった1億分の1違うだけでも
その後の結果ががらっと変わってしまう例や、
実際、ペルー沖の海水温がちょっと上がる
エルニーニョ現象が、
我々日本の天候に大きく影響を与えていることを考えると、
なんとなく「ある」気がしてくると思います。
★カオスとなる数式はたくさんある
さて、蝶々から数学に話を戻しますが、
カオス的な振る舞いをする数式は、実はたくさんあります。
また、同じ式でも最初の値や係数の設定によっては
カオス的な振る舞いをしない場合もあります。
カオス的な振る舞いを起こす数式として、
よく引き合いに出されるのが次の式です。
◆y=ax(1-x)
なんだか、ほっとするくらい簡単な数式でしょ?
aは係数で、どんな数字にしてもいいんですが
例えばaを4あたりの値にすると、
この数式は、簡単にカオス的な振る舞いを起こします。
◆y=4x(1-x)
先にも書きましたが、
この式のxに1とか2とかの値を代入していくと、
単純に「上に凸な放物線」を描く2次関数となります。
が、このxに1とか2とかの値ではなく、
前ステップのyの値を入れるとすると、
とたんにカオス的な振る舞いを始めるのです。
前ステップのyの値を入れるとは、こういうことです。
例えば、最初のxの値を0.1だったとします。
これを上の数式に当てはめると、ステップ1のyの値は、
◆4×0.1(1-0.1)=0.4×0.9=0.36
となります。
このステップ1のyの値0.36をステップ2のxの値とします。
すると、ステップ2のyの値は、
◆4×0.36(1-0.36)=0.9216
となります。
こうして、ステップ2のyの値は0.9216となり、
これがステップ3のxの値となります。
これを順次繰り返します。
◆ステップ3のyの値=4×ステップ2のyの値
(1-ステップ2のyの値)
◆ステップ4のyの値=4×ステップ3のyの値
(1-ステップ3のyの値)
◆ステップ5のyの値=4×ステップ4のyの値
(1-ステップ4のyの値)
◆ステップ6のyの値=4×ステップ5のyの値
(1-ステップ5のyの値)
たったこれだけのことで、
yの値はひどく揺れ出すのです。
実際に計算してみますと、こんな感じです。
◆ステップ3のyの値 = 0.28901376
◆ステップ4のyの値 = 0.821939226
◆ステップ5のyの値 = 0.585420539
◆ステップ6のyの値 = 0.970813326
◆ステップ7のyの値 = 0.113339247
◆ステップ8のyの値 = 0.401973849
◆ステップ9のyの値 = 0.961563495
‥‥‥‥‥‥(中略)‥‥‥‥‥‥‥‥
◆ステップ50のyの値 =0.168351377
‥‥‥‥‥‥(中略)‥‥‥‥‥‥‥‥
◆ステップ100のyの値=0.103908943
グラフにするとこんな感じになります。
この場合、a=4の初期値を0.1としましたが、
いろいろと変えてみると面白いでしょう。
いずれかをちょっと変えるだけでも、
その後の「未来」が驚くほど変わっていってしまいます。
また、単にランダムに揺れるだけでなく、
何ステップもの間ずーっと変化がなかったのに、
数万ステップ後、
突如乱れ出すなんていうカオスもありますから面白いです。
ちなみに、表計算ソフトで
いろいろなカオスの振る舞いを調べることのできる
書物がありますので、
そちらも参考にしてください
(対談形式でとても読みやすい本です。
合原一幸、黒崎政男 著
『神はカオスに宿りたもう』アスキー出版局 )
また、数字を並べられてもピンとこないという方、
実際いろいろ試してみたいけど、
プログラムは組めないしとお困りの方は、
次のようなサイトがありますから、紹介しておきます。
Chaos-game
<http://www.sun-inet.or.jp/~khirai/index.html>
★カオスは何の役に立つのか
こういったカオスの振る舞いは、
数字の世界だとか、
気象などの世界だけに起こることではありません。
最近、我々の身体の機能は
カオスだらけだということがわかってきました。
心拍数も、脳波も、呼吸も、
それに何かを覚えようとするときの脳細胞の興奮にも、
カオス的な振る舞い(=リズムがちょっとずれたりする)が
あることがわかってきています。
面白いことに、病気のときは、
このカオス的な振る舞いがなくなって、
呼吸その他が、規則的なリズムを刻み出すそうです。
つまり、正常である=カオス的に揺らいでいる
というのが我々生き物のあり方のようです。
これがどういうことなのか? 何を意味するのか?
それはまだまだ解明されていませんが、
突拍子もない考えとか、ひらめきなどというものは、
このカオスの働きによっているんじゃないかという
気もします。
最近では、NNにカオスを組み込んだモデルが
考案されています。
その名もカオス・ニューロネットワーク(
そのまんまですが)といいます。
使い方の一例として、
NNが学習中に小さい谷間(局所解)に陥ったとき、
自力でそこから脱出するためのジャンプ力として、
カオスを使うなどの方法があります。
しかし、これは我々素人には、
無縁といえば無縁の利用法ですね。
これ以外にも、
暗号やデータの圧縮技術に利用するなどの
研究もされているようです。
「で、結局、我々素人は、カオスを何に使えるの?」
と聞かれると困ってしまいます。
実を言うと、
今すぐ何かに使える代物ではないなぁというのが
個人的な感想です。
カオスという現象自体は、とても面白いんですが。
ただ、即戦力として単調な乱数の代用はしてくれそうです。
ゲームなどにおいて、
「意外性」の演出に乱数は欠かせません。
しかし、この乱数の質について
注意が払われることはあまりありません。
カオスを使うことによって、
一様で個性のない乱数に変わって、
クセのあるパターンが生まれる。
しかも、同じ初期値を使えば、
必ず同じ乱れ方をしてくれる。
それでいて、将来の値は予想不能。
これがゲームの中で、
例えばモンスターの出現頻度になったり、
あるいはシナリオの展開に関係したりすると面白そうです。
カオスを引き起こす計算式は
一般に計算量も少ないですから、
ゲームとは案外相性がいいのではと思います。
また、自動生成もの、
例えば後の章でお話しする自動作曲のようなシステムにも、
利用できそうな気がします。
ですが、これらはちょっと
ストレートな使い方すぎる気もしますね。
もう少しひねって使う必要がありそうだと思います。
|





