
ある分野を深く、深く研究する人がいます。
その人たちは「研究者」と呼ばれ、
おどろくべき知識量と、なみはずれた集中力と、
こどものような好奇心をもって、
現実と想像の世界を自由に行き来します。
流行にまどわされず、批判をおそれず、
毎日たくさんのことを考えつづける研究者たち。
ほぼ日サイエンスフェローの早野龍五は、
そんな研究者たちのことを敬意をこめて
「オタクですよ(笑)」といいます。
世界中のユニークな研究者と早野の対談から、
そのマニアックで突きぬけた世界を、
たっぷり、じっくりご紹介していきます。

森重文(もり・しげふみ)
数学者。専門は代数幾何学。
1951年、名古屋市生まれ。
京都大学理学部卒業。
同大学院修了。理学博士。
京都大学高等研究院院長・特別教授、
京都大学名誉教授。
76年に隅広秀康氏と共同研究し、
「三次元のハーツホーン予想」解決、
79年に「ハーツホーン予想」解決
(有理曲線存在定理)。
1988年に「三次元フリップ予想」解決、
「三次元極小モデル問題」を解決。
1990年に代数幾何学での功績が認められ、
日本人3人目の「フィールズ賞」を受賞する。
- 森
- これは六角形の「コーン」です。
原点から6本の線が出ています。
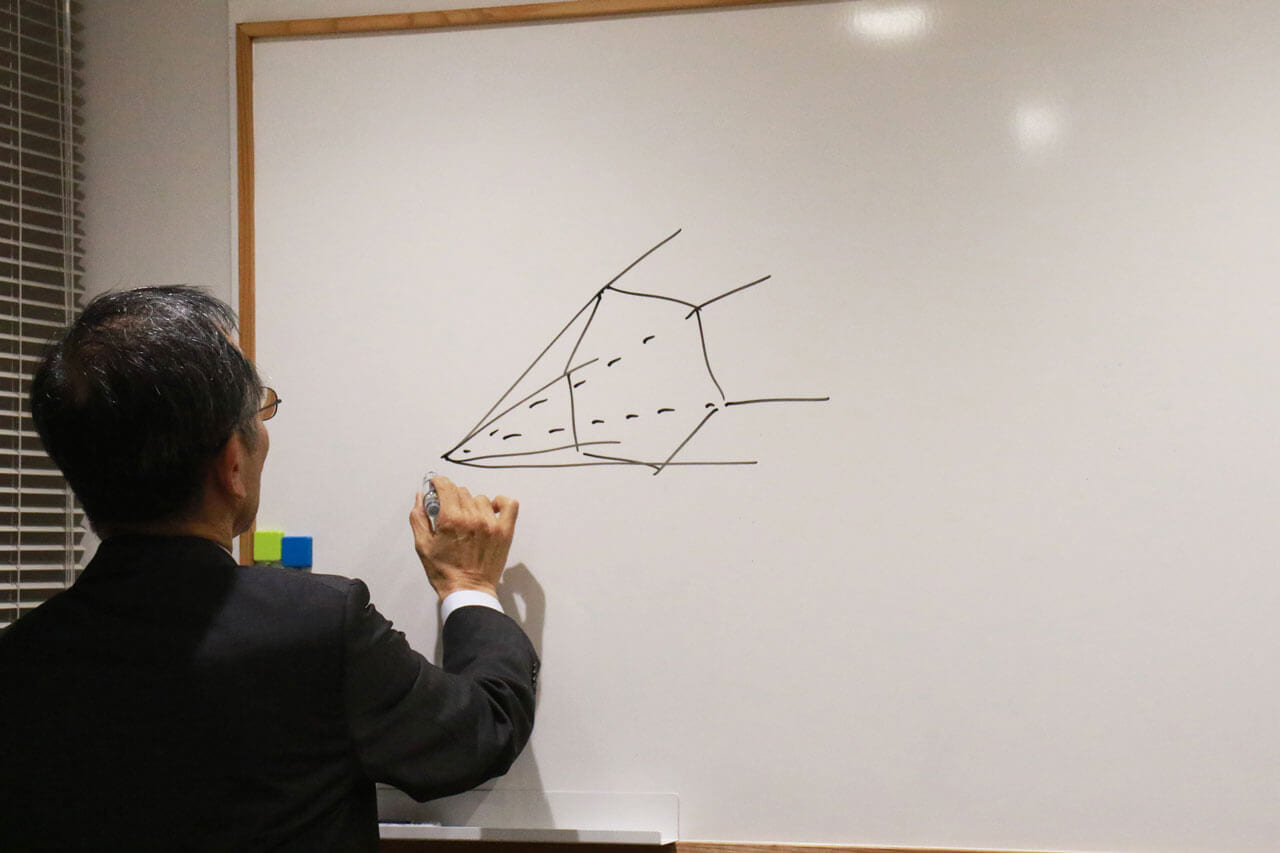
- 早野
- いわゆる「六角すい」です。
- 森
- もし六角形のところが円だったら、
円形のコーンになります。
つまり、線の中の形を見ると、
どういう形のコーンかがわかります。
- 早野
- わかるけども‥‥あの、ごめんなさい。
まず、そのコーンはどこにあるもの?
- 森
- ある代数多様体を考えると、
それは画面に描き表すことができない図形ですが、
その特徴だけを上手く抽出してきたものが
「コーン」なんです。
代数多様体という対象を、
仮想的なキャンバスに描いたのが
「コーン」と思った方がいいでしょう。
「コーン」は「仮想的なキャンバス」上にあります。
- 早野
- ええっと、つまり、
もともと「描き表すことができない図形」が、
どこかにある。
- 森
- はい。
- 早野
- それで、いま先生がお描きの絵は、
「描き表すことができない図形」の
原点と接するように線をいくつか引く、
ということですか?
- 森
- 接するようにというか、
原点からいくつか矢印を出すんです。
- 早野
- 矢印を出す?
- 森
- その矢印で張られた図形が「コーン」です。
- 早野
- うーん‥‥。
ひとまず進めましょう。
そうやって6本の線を引くと、
そこに六角形ができました。
- 森
- ただし、これは説明のために描いたものです。
ほんとうはこっちのコーンのほうが、
よりリアルに近い。
(さらにもうひとつコーンを描く)

- 早野
- それはどういう‥‥。
- 森
- 下のコーンの特徴は、
半分が円形で角張ったところがなく、
もう半分は一部が角張っています。
そういうコーンです。
- 早野
- さらにわからなくなってきた(笑)。
まず、そういうコーンを描こうというとき、
「わけのわからない図形」は数式なんですか。
- 森
- 数式で書かれています。
きちっと計算するのはかんたんじゃないけど、
計算すればこういう下のコーンのような
図形が定義されます。
- 早野
- そのコーンに接した1本1本の線も、
数式で書ける?
- 森
- 式で書けるというか、
もとの図形とはほとんど無関係です。
直接的には結びつけにくい。
- 早野
- けれども、それらはユニークに決まる。
- 森
- この図の場合だったら2本とか、
もっとあるかもしれないけど、
角張っていれば一応そこが目立つんです。 - とにかく大事なことは、
こういう「端っこの線」を決めると、
それはもとの図形の、
ある幾何学的な特徴を表していることになる。
- 早野
- 特徴を‥‥。
- 森
- 要するに、
もとの多様体についてなにか言いたい。
なにか言いたいけども、
それを見つけるのはすごくむずかしい。
だけど、もし角張ったところがあるなら、
それはもとの多様体の
「幾何学的な特徴」を表してることになる。
これらの線と図形はそういう関係です。
つまり、この線が見つかれば、
もとの多様体の幾何学的な構造を
表していることになります。
- 早野
- それは「群盲象を評す」みたいな、
ほんの一部しかわからないことじゃなくて、
その「端っこの線」があることで、
全部がわかっちゃうようなものなんですか。
- 森
- 全体ではないかもしれないけど、
大事な特徴がわかる。 - まず代数多様体を調べるには、
できるだけ小さくして調べたいという、
そういうアイデアがあって‥‥。
うーん、なんと説明すればいいのか(笑)。
- 早野
- そのコーンに接する線を引いて
「図形の特徴を表す」ということは、
先生が発明されたアイデアなんですか。
- 森
- コーンを考えるというアイデアは
広中平祐先生が考えたものですが、
「角張ってる」ことを見つけたのは私です。
- 早野
- その角張ったところに線に引くと、
その図形はなにが起きるんでしょうか。
- 森
- これは「極小モデル」を
つくるという話があるんですけど‥‥。

- 乗組員A
- わからないどころか‥‥。
- 乗組員B
- もはや「わからない」ということさえ
言えない感じです‥‥。
- 森
- 「極小モデル」をつくるには、
どうしたらよいかという指標があって。
- 早野
- ええっと、すみません。
まず「極小モデル」というのは‥‥。
- 森
- 要は、小さくする。
- 早野
- 小さくする。
- 森
- 小さくする。
- 早野
- ますますわからない(笑)。
ええっと、数式で書かれた
わけのわからない多様体っていうのは、
一般には三次元以上のもある?
- 森
- もう何次元でもあります。
- 早野
- 何次元もあって、
絵に描けないような複雑なものがある。
それを「ある手続き」にそって‥‥小さくする?
- 森
- 「小さく」というか「わかりやすく」する。
- 早野
- 「わかりやすく」する?
じゃあ、わかりやすくして、
これ以上はわかりやすくならないところまで、
どんどんわかりやすくする?
- 森
- そう。
- 早野
- ‥‥で?
- 森
- それを調べる。
- 早野
- 調べる。調べてなにがわかる?
- 森
- それはまた元のようになってるかもしれないし、
それで終わりかもしれない。
- 早野
- また元のようになる(笑)?
えっと、それはどうすれば行き着いて
「終わり」を迎えるんでしょうか。
- 森
- 行き着く先は、もう、
こういう角がなくなれば‥‥。
- 早野
- 角がなくなる。
- 森
- 角がなくなれば「極小モデル」というものになる。
- 早野
- えっと、それはつまり、
尖ったところがないという意味ですか。
円や球みたいに‥‥。
- 森
- と、までは言わないけど、
どういう曲線を持ってきても
それにそって平均すると、
プラスに曲がってるとか、
マイナスに曲がってるとか、
そういう性質のものです。
- 早野
- そういう性質のところまで
行き着くんだけど‥‥うーん。
これ以上はちょっとキケンですね(笑)。
- 森
- キケン?
- 早野
- いや、あちらが‥‥。
- 乗組員A
- (ポカーン)
- 乗組員B
- (ポカーン)
- 森
- なるほど。
- 早野
- 先生の論文の中に、
こういう表を見つけたんです。
いまの話はこのフローチャートの
ことだと思うのですが‥‥。

- 森
- ああ、そうですね。
このチャートは、
最後に行き着くまでのプロセスです。
- 早野
- いまのところの話は、
コンテンツにするには
あまりにも難解すぎますね。
ぼくもよくわかってない(笑)。
- 乗組員A
- 早野さんがわからないものを、
ぼくらがわかるはずもない‥‥。
- 乗組員B
- 頭がクラクラしてきました‥‥。
- 森
- このあたりにしておきましょうか。
私が数学の話をはじめると、
どうしてもこうなってしまいます。
(つづきます)
2019-10-01-TUE

